[I wrote this just over four years ago for a conference I never went to. I’m submitting it now in the sprit of my “Disclose This” entry, in which I promised to disclose ideas that I’d like myself and others to be able to use, and not be prevented from doing so by software patents.]
Abstract
We have a complex software application with a number of multi-media subsystem processes. We would like the application to meet certain minimum overall performance criteria. Many of the subsystem processes can be executed at varying quality levels, and these have various effects on system performance. The situation is complicated by the fact that system performance is also dependent on factors outside the software application itself (e.g., processor and network load from other applications). We apply a number of independently-operating standard industrial process-controllers to vary subsystem quality as needed so that performance criteria is met or exceeded when possible.
Summary
In our approach:
- The quality parameters of individual subsystems are automatically controlled using standard control-system methodology (i.e., PID closed-loop controller), using various overall measured system performance metrics as the controller input.
- We do not guarantee that the system performance never goes below target, but rather we adjust subsystem quality as needed to mostly meet system performance targets.
- Each controller’s responsiveness in meeting a performance target is dictated by the controller’s tuning parameters. The standard control system technology is sufficiently self-adjusting that the tuning parameters are adequate for a wide range of machines.
- The various quality levels are controlled by individual independently operating control loops, even if they are based on the same performance inputs. I.e., we treat a Single-Input/Multiple-Output system as a group of individual Single-Input/Single-Output systems.
- Some subsystems have an effect on several performance metrics. We control the quality parameters of these systems by taking a worst value produced by PID on the multiple performance measurements operating in the same control loop. Thus these loops each act as a simple Multiple-Input/Single-Output controller.
- Controller output is often pinned at an arbitrarily chosen best quality when the system has sufficient headroom, resulting in system performance that is far above the minimum targets.
- When output of a particular subsystem is pinned at an arbitrarily chosen worst allowed quality, other unpinned subsystems may continue to adjust their quality to effect performance. Whenever all applicable subsystems are pinned at their worst allowed quality, further loading degrades system performance as though there were no controllers.
Introduction
Qwaq Forums
The Qwaq Forums product is a real-time collaborative system, with a video-game-like 3D user interface. Participants see each other as avatars in a 3D workspace (e.g., a virtual conference room), as the participants simultaneously work on the same or different applications in the workspace. Communication is by means of text chat, voice (VOIP), and live streaming video (Web cameras). The applications include all standard 2D desktop applications such as Web browsers, text editors, spreadsheets, and so forth. There are also 3D applications, including simulations and animations. In particular, users’ avatars can be animated 3D human figures.
The performance demands on the system are staggering. We intend to support 50 participants or more in a single space. Each space may have 25 2D applications running simultaneously, with input accepted from each participant and the display replicated to each.
[A few years later, we did regularly support 50 and more participants. However, having 25 heavyweight cloud-based applications remained elusive for most users, primarily due to bandwidth limitations at the client when using RFB/VNC/RDP. Lighter weight built-in applications (simple text, python apps) were not a problem.]
The Control Problem
Regardless of what is happening within the system or even externally to it, we want to maintain the following performance requirements:
- Interactivity traversals of the visible scene graph must occur as often as practical, and in any case maintaining at least 10 traversals per second. This is affected by Forums activity and the other machine activity on the participant’s system.
- Latency must be no worse than a given value that varies with subsystem. For example, 500 milliseconds for voice. The network latency above a speed-of-light minimum is affected by externally imposed network path, and by the load (e.g., by ISP throttling of bandwidth).
- Other “reasonableness” metrics apply, and will be explained in the next section.
This paper does not describe what is done in the various parts of the system to be as efficient as practical (e.g., to avoid doing unnecessary work and to use efficient algorithms and formats). Despite these best efforts, the system cannot meet the minimal performance requirements when “everything is on” simultaneously at maximum quality levels.
The solution is to automatically adjust the quality of various activities. For example:
- Animation can be updated less frequently, resulting in choppier animation, but less CPU load.
- Video and remote applications can be updated less frequently, resulting in choppier texture display, but less bandwidth and less encoding/decoding CPU load.
- Streaming media such as voice and video can use a range of encodings that trade fidelity for bandwidth or encoding/decoding CPU load.
The control task is to determine a satisfying combination of subsystem quality parameters such that our performance targets are met.
But how should these quality settings be managed? The number and composition of contributing activities is combinatorially large, and constantly changing. There are no hard bounds as more users can join and they can introduce more activity. Activities can be started and stopped by any individual participant, potentially affecting all. Some activities become active on a participant’s machine only while they are in view as the user drives their avatar around within the workspace. Everyone can speak at once, or not all.
The quality parameters should vary smoothly and continuously where possible, and in any case should not change so frequently as to be distracting.
Finally, just as the control mechanism should operate correctly as different loads go into and out of use, the control mechanism should operate correctly as new subsystem processes are added within the product, and changed by different engineers.
Scope of the Control Solution
We address the control problem by using a few simple, composable, extensible, independent self-regulation mechanisms that tend towards our goals when possible. Further improvements outside this mechanism (e.g., efficiencies) should produce good results more of the time, but not make it necessary to fundamentally change this mechanism. The model here would stay in place to continue to automatically produce results during exceptional temporary situations.
For simplicity, this paper disregards server performance, and only discusses applications of the solution to the client, to control quality measurements that are the purview of that client:
- The Peer-to-Peer Croquet replication model on which Qwaq Forums is based provides for the same computations to be performed on each participating machine. Such “global” parameters are not addressed. Instead, activity that is purely cosmetic and which does not affect collaborative correctness (e.g., animation update frequency,) is pushed outside the Croquet replication model so that individual participating machines can control their own quality values using the dynamic control system, without effecting others. How such computation is removed from Croquet replication is not within the scope of this paper.
- There are some activities, such as external applications, that are handled something like having a non-user “peer” interacting with the application, and injecting the results into the replicated Croquet collaboration. The quality parameters of such activity processes can be individually controlled using the same kind of mechanism described here, but we do not present any examples.
- The discussion here is based on one machine controlling a quality metric that affects the experience on that machine. However, there are several process that have an impact on multiple participants. Examples are the external applications just mentioned, and streaming video encoding that must be received and decoded by all viewing participants. This could maybe be handled by having each participant reporting their performance to the replicated collaboration, which the injecting participant would then convert to a composite worst-case performance metric for automatic control of quality parameters. However, we have not yet done that. Instead, we have developed a “reasonable output” proxy measurement based on an estimate of the composite performance impact. For example, a participant injecting streaming video into a Forum measures the encoded camera output bandwidth, and uses this as one of the performance measurement inputs.
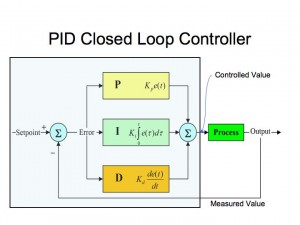
Closed-Loop Control: PID
Multi-Input/Multi-Output control systems (MIMO) are hard – the theory is not well developed – but Single-Input/Single-Output systems are pretty well understood within the literature. SISO has a number of tools available to smoothly vary a parameter to reach a desired performance result, without big jumps and oscillations and other nasty stuff. The most commonly used is the PID closed-loop controller. It does not give optimal results, but it does give correct results over a wide set of circumstances, and that’s good enough for our purposes. We had been thinking of our task as an optimization problem: “How do we crank the knobs to achieve the best performance (with a hard floor) while meeting quality needs.” The first insight is to recast this as a simple SISO control problem, where the floor is our setpoint.
For example, the number of animation updates per second can be continuously varied. The more animations, the more computation must be done, and this will lower the net interaction rate that can be processed (frame rate, R frames per second). We want to make sure we achieve R = 10 fps, so we make a controller with that as the measured value setpoint. Animation is not the only thing effecting R, but it is one of things. The second insight is that the animations/second can only vary over a certain reasonable range. The controller works within that range to achieve the result, or it just pins on the best or worst quality, and we then hope that some other controllers can do the rest.
PID controllers are pretty simple. The controlled value is a function of three terms:
- a term directly Proportional to the “error”, or (setpoint – measuredValue).
- a term proportional to the Integral, or accumulation of error, and
- a term proportional to the Derivative, or current rate of change of error.
controlledValue(t) = KP*e(t) + KI*integral(e(t)) + KD*(de/dt)
Interpretation of Input/Output and Measure/Controlled
measured value = a realtime performance measurement
= input to the controller
= the production “output” measurement of the whole system or “plant.”
Higher numbers mean “more output” and reflect a more desirable experience for users.
controlled value = a quality parameter or (inverse) “knob” that we can adjust
= output of the controller
= the input to the subsystem process or “plant”, which affects the plant output. (Hence “closed-loop” controller.)
The way error is defined in the literature, (setpoint – measuredValue,) a positive error means we need to crank up the plant to meet our performance target. So cranking up the controlled value knob means more plant output, and in our case, lower quality for the process being controlled. For example, in controlling animation, the controlled value is the number of rendering frames per animation update: higher numbers mean more overall system performance, but lower animation smoothness. (It is tempting to invert this so as to be able to interpret the controlledValue numbers more intuitive as “quality” rather than “inverse quality.” So far I have chosen to be consistent with the literature and so that the different control loops can have similar looking software.)
The Basic Loop
The basic loop in software is quite simple:
doControlLoop: lastError accumulation: lastAccumulation
"KP, KI, KD, and DT are numeric tuning parameters.
MeasuredValueSetpoint is a tunable frame rate target, e.g., 10."
| error accumulatedError changeInError p i d computedValue |
error := MeasuredValueSetpoint – self measuredValue.
p := KP * error. "term is Proportional to error"
accumulatedError := error * DT + lastAccumulation.
i := KI * accumulatedError. "term is Integral of error"
changeInError := (error - lastError) / DT.
d := KD * changeInError. "term is Derivative of Error"
computedValue := p + i + d.
self controlledValue: computedValue.
(Delay forSeconds: DT) wait.
self doControlLoop: error
accumulation: accumulatedError.
You’ll notice that multiplying or dividing by DT could be incorporated into the KI and KD coefficients if DT is constant. In fact, some of our control loops do not have constant DT. (See “Iterating and Obtaining Samples”, below.) There are also a couple of ways in which the integral term could be written (e.g., with KI applying to the whole or just the new part). These different coefficient uses are referred to as “Ideal Form” and “Standard Form” in the control-systems literature.
Variations on the Basic PID Control Loop
Pinning the Control Knobs
In industrial control systems, the controlled value can be any computed value, but the physical limitations of the plant will effectively provide limits. In our software system, we need to explicitly cap these parameters ourselves:
computedValue := p + i + d "this part is as before, adding…" min: MaxControlledValue max: MinControlledValue.
The Min and MaxControlledValue act as “pins” on our quality control knobs. For example, when controlling the number of rendering frames per animation update, we have a MinControlledValue of 1, and a MaxControlledValue of 10.
These caps are important: We don’t really want performance to be at our MeasuredValueSetpoint most of the time.
- We want more if possible. So rather than letting quality get “better” and better to use up performance, we pin our inverse-quality knob with MinControlledValue. For example, in animation, we don’t need less than one rendering frame per animation update (i.e., it would be silly to update the animations faster than overall rendering). So when there’s plenty of headroom in the system, we expect each computedValue to be pinned at MinControlledValue and our measuredValue to be higher than our MeasuredValueSetpoint. Thus we hope that most of the time, the control loops are not even operating! They just kick in when they need to.
- There comes a point at which it isn’t worth further degrading the quality of some particular subsystem process. If we’re still not meeting performance requirements at that point, it is really time to look elsewhere. So we also have a MaxControlledValue inverse-quality knob limit, above which the controller will not further attempt to improve performance. At that point, it is up to some other subsystem process controller to help out, or else the measured performance value will continue to degrade.
Anti-Windup
For various reasons, the system might not respond for a while: the tuning might respond slowly, the entire system might be paused, etc. The integral term is much like a spring that cand be wound up, and this can result in the accumulation of a large error that takes a while to work off – especially with our MaxControlledValue pin. So we include what is called an “anti-windup provision” in the literature:
accumulatedError := measuredError * DT + lastAccumulation "the above is as before, adding…" min: 10*MeasuredValueSetpoint
max: -10*MeasuredValueSetpoint.
Deadband
In the controllers we have made so far, the output varies smoothly enough. However, some controllable subsystem knobs should not be constantly changing. For example, we might make an “encoding indicator” knob that uses one kind of video encoding if the controlled value (video encoding frame rate) is between, say, 1 and 2, another if it is between 2 and 4.5, and a third if it is between 4.5 and 10. We don’t want to change encodings too often, so it may become necessary to add what is called a “deadband limit” on the controlled value:
(computedValue - self controlledValue)abs > DeadbandLimit
ifTrue: [self contolledValue: computedValue].
MISO
Some quality controls affect multiple performance characteristics, and so we must consider multiple measured value controller-inputs in computing a single inverse-quality knob controller-output (MISO).
For example, consider the frame rate at which a participant’s Web camera is injected into the computation:
- The more frames to be encoded, the more that participant’s processor will get loaded.
- The more frames sent on the wire, the more that participant’s packets may be delayed from throttling by network management.
- We really need to know if we’re slowing down other folks, but we do not yet include such feedback between participants. Instead, we use camera output bandwidth as a proxy indicator of how much damage we may be doing to other participants’ performance. Note that the bandwidth usage is not an easily computable function of frame rate, as it depends on how much the actual image is moving around between any two frames.
We handle this by computing a computedValue1, computedValue2, etc. within the same control loop. Each measuredValueN is a different performance measurement.
error1 := MeasuredValueSetpoint1 – self measuredValue1.
p1 := KP1 * error1.
...
computedValue1 := p1 + i1 + d1.
error2 := MeasuredValueSetpoint2 – self measuredValue2.
p2 := KP2 * error2.
...
computedValueN := pN + iN + dN.
computedValue := ((computedValue1 max: computedValue2)
max: computedValueN)
min: MaxControlledValue
max: MinControlledValue.
Recall that the objective is not to stay at the minimum performance when we have sufficient headroom, nor to produce the absolute optimum quality for a given performance. The insight here it is realize that it is sufficient to merely use the worst result from the N computedValues in order to mostly keep all the N performance metrics at or above their targets.
Iterating and Obtaining Samples
The usual rule of thumb is to take your sample measurements about 10x faster than the response time you want. That is, if you want the system to adjust a process within, say, one second, then DT ought to be no larger than 0.1 seconds.
How the control loop actually runs varies with the subsystem being controlled. We currently write a different version of the basic “doControlLoop” method for each controller. For example:
- For controlling camera frame rate, we fork off a separate #doUpdateRate process whenever we setupCamera. This process has an explicit loop that does not exit until we destroyCamera. At the bottom of each iteration of the loop, we explicitly Delay for DT seconds.
- For animated figures, we have a single controller that controls overall number of rendering frames per animation update, used by all animated figures. The #doAnimationUpdateRate method is explicitly called once at the start of each rendering pass. Thus “dt” is 1/frameRate when animation is happening, and our purpose is to keep frame rate above 10fps. So “dt” is less than 0.1 seconds. Note that there is no separate control loop process here, as it happens serially with rendering.
The interpretation of assigning #controlledValue: varies. For the camera frame rate, the controller is a method for each QVideoCameraManager instance, and changing the controlled value alters the current frame rate of the camera it controls. For figure animation, changing a number of renderings per animation update figure used by all TAnimatedMesh instances.
The details of obtaining measuredValue also varies. Some controllers use counters that are shared across many subsystems, while others have individual counters. Some DT are such that we cannot be sure of a measured value to be counted on each iteration, and so it is necessary to use a moving window average (which reduces response time). The details are out beyond the scope of this paper. (But see QFrameRate, TWindowedStatistics, TTrafficCounter and QCounterRate.)
Tuning
In control-systems, “tuning the system” does not mean making it more efficient, but rather picking values for the coefficients KP, KI, and KD. Bad values will cause the measuredValue to not reach the setpoint, or to oscillate between values. Particularly good values cause the measuredValue to stabilize at the setpoint more quickly.
In rocket science, you have to pick these before the spacecraft flies, but in our case, we get to experiment.
Our control loops all have a means of transcripting measuredValue, controlledValue, p, i, and d terms and so forth. Of course, writing data to the screen effects performance, so this recording bulks up results (e.g., in batches of 40 iterations) and reports them in a batch. Even so, the first few results of each batch are affected by the previous report. (We probably should stop controlling for a while after each report.)
The coefficients, setpoints, and limits are implemented as class variables so that they can modified on the fly by a developer in order to observe the result of the change.
There are various techniques that have been written up. In general, one tunes one coefficient of one loop at a time. For example, unnecessary subsystems are turned off so that the system is operating at the MinControlValue for all other controllers. For the controller being tuned, a setpoint is chosen that is in the middle of the current range of values on the developer’s machine, in order to force the controller to operate in its non-pinned range. (This is why we do not use the same global MeasuredValueSetpoint for each controller, even if they are the same value.) Multiple inputs for a MISO controller are turned off by adjusting their setpoints out of the way, or turning their coefficients to zero.
The P term has the most impact in reaching the setpoint quickly, so KP is tuned first, with the other coefficients at zero. The system might not be able to reach the setpoint with P alone – it may need I. So the goal at this stage is merely to make KP as high as possible without the result oscillating. One usually varies KP by decades until the criticial oscillating point is found, and then backing off to about 0.6 of that.
Then the I term is used to provide an offset to the computedValue that will allow it to reach the setpoint.
The D term is often zero. It can be used to dampen oscillations so that KP can be a little higher than it would otherwise be, for faster response time.
Precision is not required. If the figures are off a bit, it just takes a little longer to reach the setpoint after a disturbance, or the quality varies a bit more than it needs to. This is what allows us to encode parameters into the application distribution and have them work across a wide range of machines.
As changes are made within a subsystem, and in other subsystems that run simultaneously, we don’t expect the basic machinery to need changing, but we do expect that we should to re-tune from time to time.
Future Work
Experience
[Four years ago, I wrote that we need to gain experience with how this worked in practice. As it turns out, I checked the tuning for the next few releases, on a MacBook Pro and a weak Windows computer. The tunings turned out to be very stable, rarely requiring adjustment. After a while, I stopped bothering to check.
Tuning Across Machines
We could develop some tools to quickly exercise each controller on a given test machine, to verify that the tuning is acceptable.
Tuning itself can be automated, and there are commercial tuning packages used in industry. However, the values proved to be stable enough that we never bothered.
SIMO and Interactions Between Controllers
We already have two controllers that both affect the same measured value – frame rate. This is a Single Input, Multiple Output system (SIMO). We don’t want these controller outputs to interfere with each other such that they make adjustments (to different subsystems) that cause each other to oscillate or pin.
We think that this is unlikely if they have different response characteristics – different coefficients, and with different sets of multiple inputs going into the computedValue.
If it does happen, we will need the prioritization discussed next.
[It turns out that such a problem was never observed.]
Meta-Control of Limits
Even without oscillations or other bad interactions, we may find that we want more control over how one subsystem degrades compared with another.
A simple way to prioritize multiple controllers is to have them use different setpoints – one kicks in before another. We have not applied this yet to enough different quality knobs that this has become necessary.
When we do, we may find that we want to use different Min/MaxControlledValues when operating within different regimes. These parameters might be varied automatically by yet another controller. The general field called “adaptive control” is difficult, but I think we can apply the same hierarchy of hacks recursively:
- If there’s a conflict between between a specific set of tuned controllers, prioritize them by using different setpoints.
- Resolve remaining conflicts among N controllers by breaking N-1 of them into a operating regimes bound by a Min/MaxControlledValue. Define N-1 new meta-controller whose output determines the operating regime for the corresponding controllers.
- By construction, this resolves conflicts among the N originally conflicting controllers, but may result in conflicts among some subsest of the N-1 new metacontrollers. If so, recurse.